Time Travel
Posted by Tom Brown on Wed, 13 Mar 2019
The scans illustrate typical behaviour of graphs, the equations in themselves are not important just the shapes. The sketches are not accurate one needs only to understand the characteristic properties. With this blog I am trying to explain some concepts to a layman.
page 1
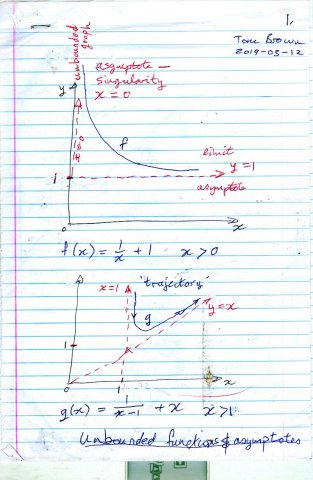
These two sketches illustrate some types of long term behavior of curves such as bounded or unbounded graphs, singularity, limits and asymptotes.
page 2
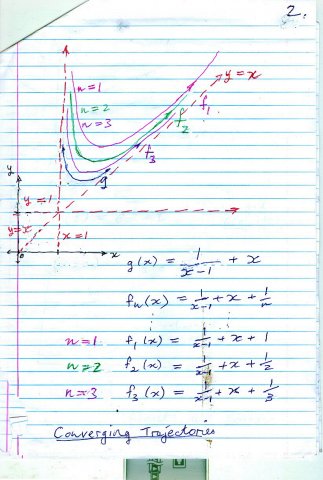
A sequence of trajectories f_n can converge to the same limit function g. Each is distinct, in our situation they can never intersect each other nor g.
page 3
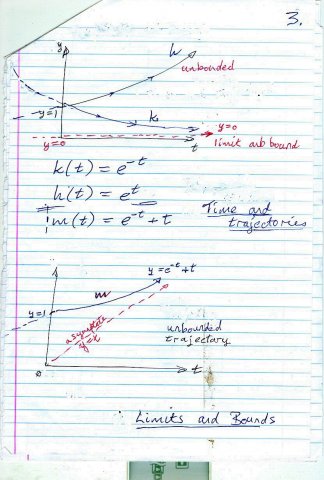
The exponential function h is unbounded and doesn't have an asymptote whereas k does and k is bounded from below, m is also unbounded but does have an asymptote, y = t ; t > 0
A trajectory is a function of time, which is positive.
page 4
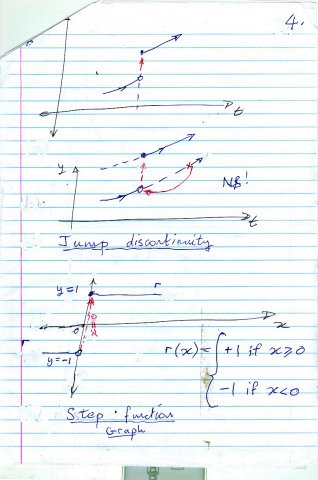
This is the essence of our speculated time travel and it is explained in more detail in the ABC note.
Finally, a step function is a concrete example of this kind of discontinuity: y is -1 if x is negative ; y is +1 otherwise, i.e for x non-negative.
~
These figures belong to the note Logic of Time Travel
https://www.abctales.com/story/tom-brown/logic-time-travel
- Tom Brown's blog
- Log in to post comments
- 1120 reads